ソリッドワークス/SolidWorks、AP100、プログラム、TIG,CO2,手棒、板金
スケッチは、平面でないといけません。これを利用すると平面かどうか、直線になっているかどうかがわかる。これは、板金に変換する時に必要なことがある。 動画は、初めに円錐の面をクリックしている。そのごいろいろとクリック。展開の … “平面（直線）の位置を探す方法” の続きを読む
2次元的に展開図を描いたのはこちら 円錐を作って シェル化（普通というか一番簡単） 展開のための細長い四角を抜く 何度か失敗している。 展開のためのカットは、最後にして板金の展開を使うのがいいようだ。 先に展開用の細長い … “放射線法 斜めにカットした円錐 板金タブ” の続きを読む
2次元的に展開図を描いたのはこちら
円錐を作って
シェル化（普通というか一番簡単）
展開のための細長い四角を抜く
何度か失敗している。
展開のためのカットは、最後にして板金の展開を使うのがいいようだ。
先に展開用の細長い四角を抜いているとだめ。
斜めにカットとかは先にする。
スケッチで、展開用の細長い四角のカット線に線を引いてしまう。
これが問題なんだろう。
あえてというより、展開図は、２次元CADの方が簡単。AP60、AP100をやってる人は展開図がすぐにわかるだから、ソリッドワークスで立体図は時間がかかる。 ソリッドワークスを部品（立体図）を書かないで、２次元的に使う。J … “放射線法 斜めにカットした円錐 あえて2次元CADで” の続きを読む
あえてというより、展開図は、２次元CADの方が簡単。
AP60、AP100をやってる人は展開図がすぐにわかる
だから、ソリッドワークスで立体図は時間がかかる。
ソリッドワークスを部品（立体図）を書かないで、２次元的に使う。
JW-CADなんかでもいいが、使い慣れたソリッドワークスでという感じ。
ソリッドワークスで２次元CADする場合は、
拘束
を使うのがミソ。ポイントでしょう。
正面図と平面図の用意
平面図に相関線を入れるために
補助線を入れる。
展開図を描くのに相関線は必要ないが。
平面図に相関線を入れる
展開用に正面図をコピーして、展開準備
円周を１２等分するが、実際の長さより短い。
円弧を直線に置き換えているので。
でも、展開図ではよくやる。
２次元CADなんで計算でしてもええが。
ここでは、手書き風。
展開図に円弧を描く
スケッチのスプラインっていうのを使う。
完成
平面図の相関線に相当するところを描く
普通に３次元ではこちら
あえて２次元CADで三角形法はこちら
たった２日間だがありがたい。土日も含めて４日間。結構、下書きがあるので整理するか公開するほどでもない下書きは、公開より多い。１行程度の下書きは消えていく。
この展開図は、シェル化から板金に変換が簡単。スケッチだけ、前準備 シェル化、板金に変換 展開図は、放射線法でもできる。しかし、放射線法って、長いコンパスがいるかな。電卓で４つの台形の展開図を作るのはこっち。これなら、コン … “三角形法 シェル化 板金に変換” の続きを読む
ソリッドワークス/SolidWorksの板金タブの展開を使った例はこっち
円筒を斜めにカット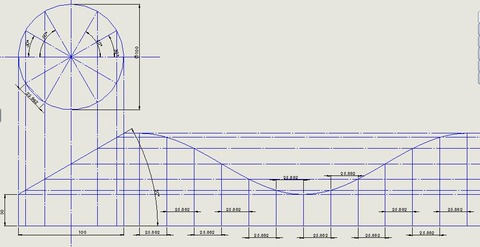
円周を１２等分するが、実際の長さより短い。
なぜなら
円弧を直線に置き換えているので。
２次元CADを使っているので直径ｘ円周率／１２の方がええかも。
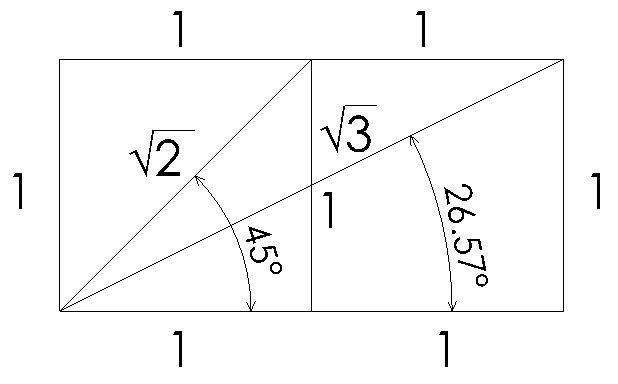
展開図の話で三角定規１：√２とか√３とかきりのいい数字というか覚えやすい数字があてはめられる。 この三角定規は、正方形と正三角形からできている。それぞれ半分にする。 直角二等辺三角形は、正四角形/正方形からできる。正方形 … “直角二等辺三角形は、正方形を探せ” の続きを読む
展開図の話
で
三角定規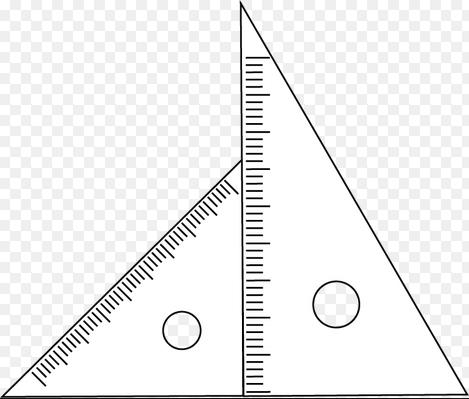
１：√２とか√３とか
きりのいい数字というか覚えやすい数字があてはめられる。
この三角定規は、正方形と正三角形からできている。それぞれ半分にする。
直角二等辺三角形は、正四角形/正方形からできる。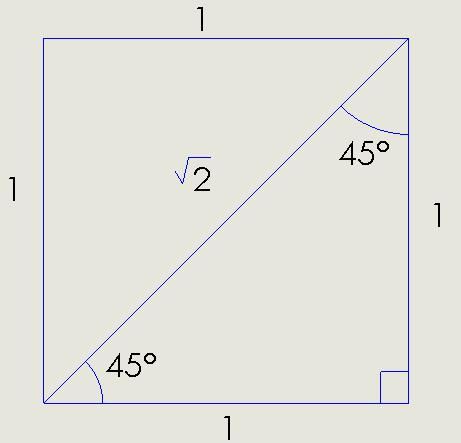
正方形からできていると
覚えると
√２が関連できる。
12+12=(√2)2
もひとつ
正三角形からできている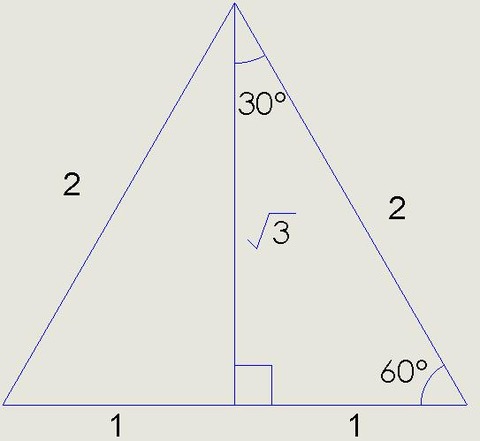
こっちはあまり展開図には使わないかな？
ポイントは正方形と正三角形からできているってこと。
２つの正方形？？？？じゃない？違います。１，２，√3となってるけど√3と2の辺の位置が違います。2の位置にご注意。正三角形からできていることを知ってれば２の位置は間違いません。【超重要】３０°と６０°の三角比/三角関数ですが、三角定規くらいは覚えましょう。覚えるのは「正方形」と」「正三角形」です。
さて、
正方形はよくみかける。
これは平面図、上から見た図だ。
四角錐のとがったぶぶんを水平に切り取った感じの物。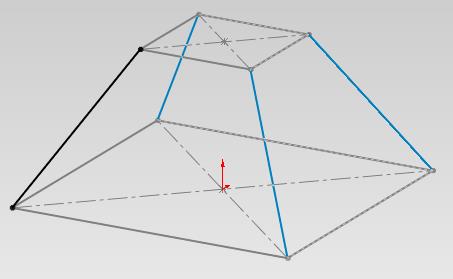
これを上から見ると。平面図。
正方形なら１：√２の関係が使える。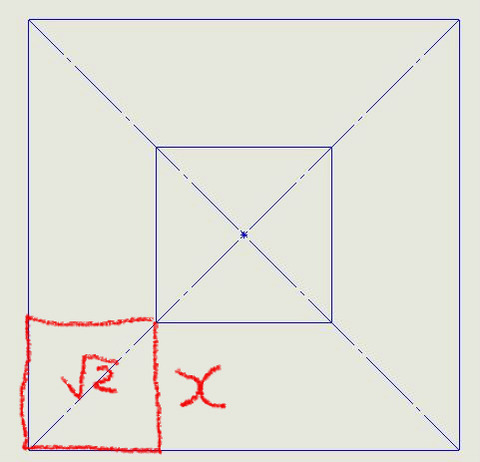
ｘの値は図面に書いてある。
その斜め線はｘを√２。
１．４倍すればいい。
ただ、
この１．４倍した寸法は、底辺の長さに相当する。
これに高さがわかれば
ピタゴラスの定理で斜めに上がっている線の実際の寸法がわかる。
立体的に見ると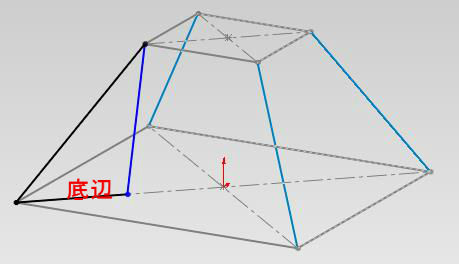
求めたい斜めの実際の線の長さの2乗＝底辺の2乗＋高さの2乗
直角三角形で
一番長い辺の2乗＝他の短い辺の2乗＋他の短い辺の2乗
ピタゴラスの定理
三平方の定理の定理の話をしていて （ピタゴラスの定理ともいうらしい） 直角、９０°と辺の関係がとっても大切だということに気づいた。 あ、そう。 っていうくらいの話ですが、熱い現場での脳は迷うんですね。 これを何となく程度 … “三平方の定理は直角がないとだめ” の続きを読む
三平方の定理の定理の話をしていて
（ピタゴラスの定理ともいうらしい）
直角、９０°と辺の関係がとっても大切だということに気づいた。
あ、そう。
っていうくらいの話ですが、熱い現場での脳は迷うんですね。
これを何となく程度の記憶だと間違う。気づかすに切断してしまうと、よけいな時間がかかってさらに暑くなる。
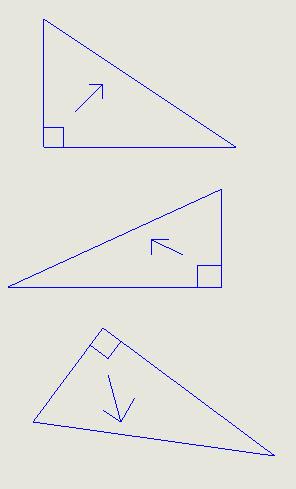
いろいろ回転しているのがミソです。
直角三角形でなと
三平方の定理は使えない。
何となく三角形だから三平方の定理が使えるなんって思ってはいけない。
直角/90°を探しましょう。
直角に対している（向かい）の辺が、一番長い辺。斜辺と言ったかな？
とにかく、一番長い辺。
なぜなら、
三角形の角度は合計して１８０°。
直角とは９０°だから３つある角度の半分を使っている。
だから
９０°の向かいの辺は、一番長い。
これが分からないとCがどの辺？なの？？となる。
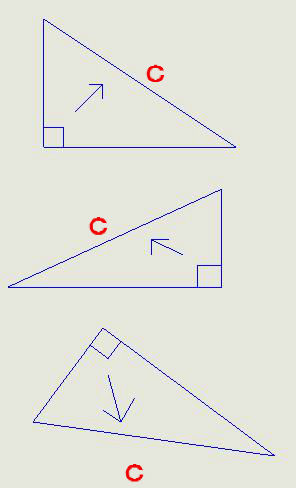
a,bは書いてない。
どっちだっていいのだ。
（sin,cos,tanの三角比/三角関数ではないのだ）
Cが大切。
ここで終わっては、いけない。
問題を作って確かめる。
問題１
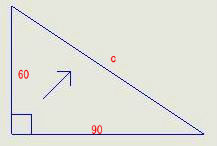
１１７００のルートは、108.16653826391967879357663802411
＝108.16653826391967879357663802411
ルートって平方根。の根root
問題２
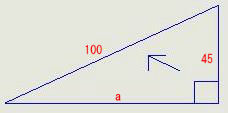
a2+452=1002
a2=1002-452
√12025 ＝109.65856099730654408274035848064
問題３
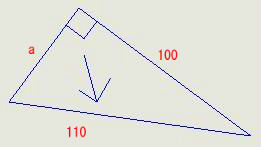
a2+1002=1102
a2=1102- 1002=22100
a=√22100=148.66068747318505522612008213931
ところで、
直角が見つからない！
そんなときは、
直角になるように線を追加して直角三角形を作りましょう。
