三平方の定理の定理の話をしていて
（ピタゴラスの定理ともいうらしい）
直角、９０°と辺の関係がとっても大切だということに気づいた。
あ、そう。
っていうくらいの話ですが、熱い現場での脳は迷うんですね。
これを何となく程度の記憶だと間違う。気づかすに切断してしまうと、よけいな時間がかかってさらに暑くなる。
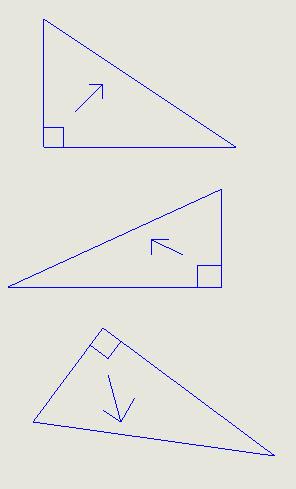
いろいろ回転しているのがミソです。
直角三角形でなと
三平方の定理は使えない。
何となく三角形だから三平方の定理が使えるなんって思ってはいけない。
直角/90°を探しましょう。
直角に対している（向かい）の辺が、一番長い辺。斜辺と言ったかな？
とにかく、一番長い辺。
なぜなら、
三角形の角度は合計して１８０°。
直角とは９０°だから３つある角度の半分を使っている。
だから
９０°の向かいの辺は、一番長い。
これが分からないとCがどの辺？なの？？となる。
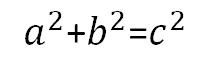
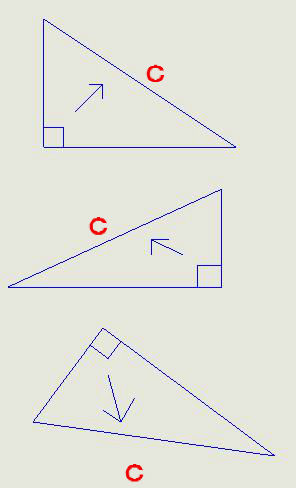
a,bは書いてない。
どっちだっていいのだ。
（sin,cos,tanの三角比/三角関数ではないのだ）
Cが大切。
ここで終わっては、いけない。
問題を作って確かめる。
問題１
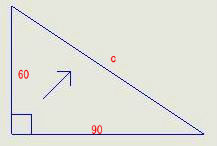
１１７００のルートは、108.16653826391967879357663802411
＝108.16653826391967879357663802411
ルートって平方根。の根root
問題２
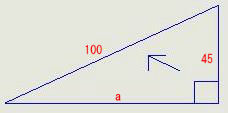
a2+452=1002
a2=1002-452
√12025 ＝109.65856099730654408274035848064
問題３
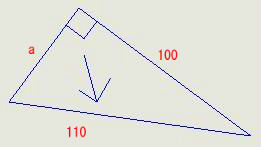
a2+1002=1102
a2=1102- 1002=22100
a=√22100=148.66068747318505522612008213931
ところで、
直角が見つからない！
そんなときは、
直角になるように線を追加して直角三角形を作りましょう。