直角二等辺三角形は、正方形を探せ

展開図の話
で
三角定規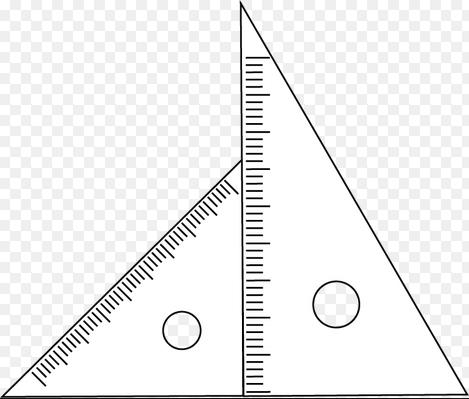

１：√２とか√３とか
きりのいい数字というか覚えやすい数字があてはめられる。

この三角定規は、正方形と正三角形からできている。それぞれ半分にする。

直角二等辺三角形は、正四角形/正方形からできる。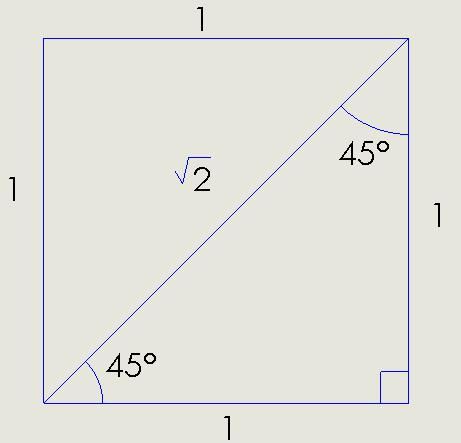

正方形からできていると
覚えると
√２が関連できる。
12+12=(√2)2
もひとつ
正三角形からできている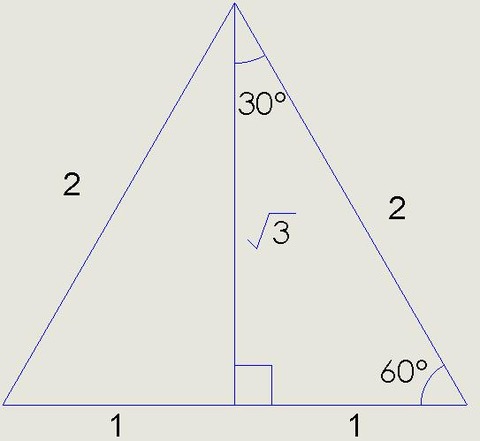

こっちはあまり展開図には使わないかな？

ポイントは正方形と正三角形からできているってこと。

２つの正方形？？？？じゃない？違います。１，２，√3となってるけど√3と2の辺の位置が違います。2の位置にご注意。正三角形からできていることを知ってれば２の位置は間違いません。【超重要】３０°と６０°の三角比/三角関数ですが、三角定規くらいは覚えましょう。覚えるのは「正方形」と」「正三角形」です。

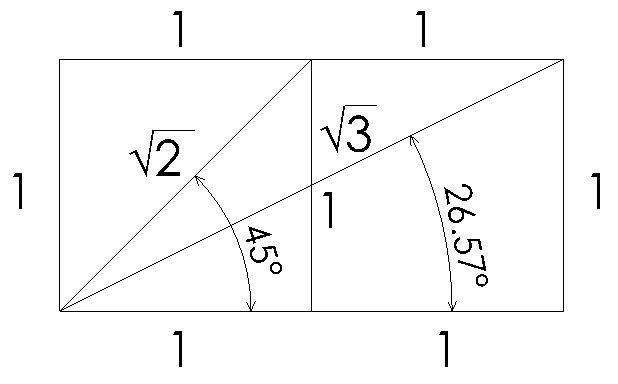
さて、

正方形はよくみかける。
これは平面図、上から見た図だ。
四角錐のとがったぶぶんを水平に切り取った感じの物。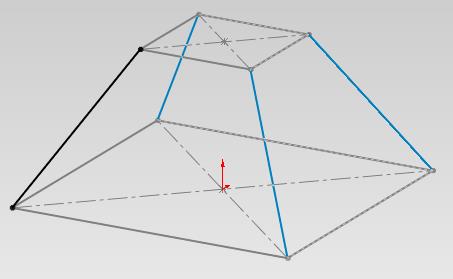

これを上から見ると。平面図。
正方形なら１：√２の関係が使える。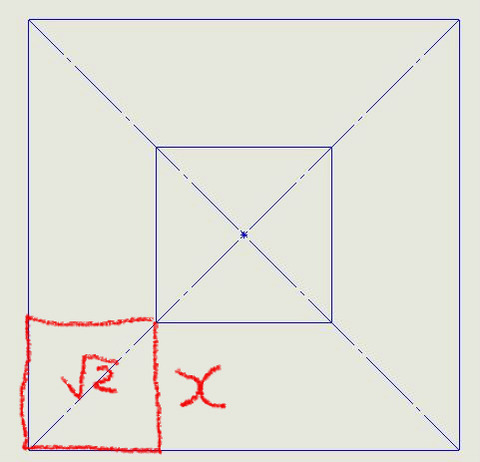

ｘの値は図面に書いてある。
その斜め線はｘを√２。
１．４倍すればいい。
ただ、
この１．４倍した寸法は、底辺の長さに相当する。
これに高さがわかれば
ピタゴラスの定理で斜めに上がっている線の実際の寸法がわかる。
立体的に見ると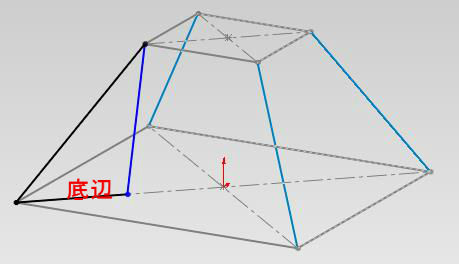

求めたい斜めの実際の線の長さの2乗＝底辺の2乗＋高さの2乗

直角三角形で
一番長い辺の2乗＝他の短い辺の2乗＋他の短い辺の2乗
ピタゴラスの定理